Formal Languages

  Languages (Linguagem) are a fundamental concept in computer science, defined by an alphabet (alfabeto) and words (palavras, cadeia de caracteres). The alphabet is defined as a basic abstract entity, containing a finite amount of letters and digits. Therefore, the infinite set is NOT an alphabet. However, the empty set ∅ is an alphabet.

  An example of alphabet is the set {a, b, c}. A more practical example of an alphabet is the set of all symbols used to write a program. Writing a C program, for example, includes letters, numbers, special characters like ">", "/", etc. The binary alphabet is the domain of values for a bit, such as {0, 1}. It is analogous to the inner workings of real computers.

  While an alphabet, represented by Σ (sigma) is a finite sequence of symbols, a symbol-less string would be represented by "ε" (Epsilon). This symbol represents an empty string or word, as well as the neutral element (elemento neutro) in formal languages, meaning it does not change words in any way. Prefixes and sufixes are examples of subwords, or strings of symbols contained within a larger string / word. With the word "abcb" as an example, made with the alphabet {a, b, c}, we have the prefixes "ε", "a", "ab", "abc" and "abcb".

  Concatenation is a binary operation on a set of words. It associates a pair of words, forming a new one from the juxtaposition of the first with the second. Concatenating any word with ε results in the same word, unchanged. Concatenation is also associative, so concatenating the words " v(wt) " and " (vw)t " will yield the same result. The parentheses may be omitted.

  If we have two words, "v = baa" and "w = bb" from the alphabet Σ = {a, b}, then the concatenation of two will look like such: vw = baabb. Other interactions with concatenation include:

• wⁿ will concatenate w with itself n times. Can be represented recursively as wⁿ = ww^n-1, n > 0
• w⁰ = ε, the neutral element
• a⁵ = aaaaa, a being a symbol of an alphabet.

  If we have an alphabet Σ, then:

• Σ* is the set of all possible words on Σ
• Σ⁺ = Σ* - {ε}

  The alphabet Σ* is inductively defined. The base of the induction is: ε ∈ Σ* -> for every x ∈ Σ, x ∈ Σ*. Each step of the induction is: If u and v are words of Σ*, then the concatenation uv is a word of Σ*. Thus, the set of all words can be formed by the alphabet Σ. Example:

if Σ = {a, b}, then:
• Σ⁺ = {a, b, aa, ab, ba, bb, aaa, aab, ...}
• Σ* = {ε, a, b, aa, ab, ba, bb, aaa, aab, ...}

  The length of a word is represented by |w|. It is a function of domain (domínio) Σ* and range (codomínio) N. It returns the number of symbols in a word. For example: |abcb| = 4 and |ε| = 0.

  A formal language is a component to an alphabet. The set of parts of Σ*, 2^Σ*, represents the set of all languages on an alphabet. An example of language is every program made in Pascal, or C, or Python, for example. The set of all programs is infinite.

  Grammar (gramática) is a finite set of rules which, when applied successively, generate words. The set of all words generated by a grammer defines a language. For example, with the rules of C programming, you can generate programs in that language. It applies to programming languages the same way it does to natural languages, like English. Chomsky's Grammar is, then:

G = (V, T, P, S)
• V is the finite set of variable / non-terminal symbols.
• T is the finite set of terminal symbols of V.
• P is the union of V and T, a finite relation.
• S, distinct of V, is the initial symbol / variable.

  Derivation (derivação) is the substitution of a subword according to a rule of production. It is denoted by an arrow, ⇒, with a domain in (V∪T)⁺ and range in (V∪T)*. ⇒* denotes a transitive and reflexive relation, ⇒⁺ denotes a transitive relation, ⇒ⁱ denotes i steps of successive derivation.

  if G = (V, T, P, S), then we can use the example:

• V = {N, D}
• T = {0, 1, 2, ..., 9}
• P = {N → D, N → DN, D → 0 | 1 | ... | 9}

  This way, the set of natural numbers is syntactically-generated, although leftmost 0s are distinct (123 is different to 0123). Another example that can be shown is the derivation of the number 243:

• N ⇒   N → DN
• DN ⇒   D → 2
• 2N ⇒   N → DN
• 2DN ⇒   D → 4
• 24N ⇒   N → D
• 24D ⇒   D → 3
• 243
Therefore: S ⇒* 243 and S ⇒⁺ 243.

Automatons

  Finite Automatons (Autômatos Finitos) are state machines with a finite number of states. They are efficient algorithms that read inputs one symbol at a time. Any finite automaton is equally efficient. Each state in a state machine contains only previous information, necessary to determine the next step.

  States in a finite automaton may be Non-deterministic (Não-determinista) when they output a random value. The random choice can be within a system or outside of it, but its main point is helping to reduce the complexity of an automaton for easier understanding. Non-deterministic automatons can also perform "empty moves", represented by ε, usually symbolizing that a state machine will connect to another one at a random moment, without changing the inputted string. Deterministic Automatons (AFDs) can become Non-Deterministic Automatons (AFNs), and vice versa.

  The input of an Automaton is the "tape" (fita), consisting of a finite amount of symbols to be processed. The Automaton will read each symbol, one at a time, and determine what the next state will be based on the previous one. The symbols of the tape follow the rules of Formal Languages, such as belonging to an alphabet, forming words, etc. The tape is read by the Automaton's control unit. Automatons are not capable of storing any data, so its "memory" is simply the current state.

  A Partial Function (Função Parcial), is a state machine in which not all states and transitions are plotted out, such as a state machine going from state 1 to state 2 with input A, with no consideration for other inputs.

M = (Σ, Q, δ, q0, F) represents a Finite Automaton, where:

• Σ is the input alphabet.
• Q is the set of possible states of the automaton.
• δ (delta) is a program (function) or transition function (parcial function).   δ: Q x Σ → Q
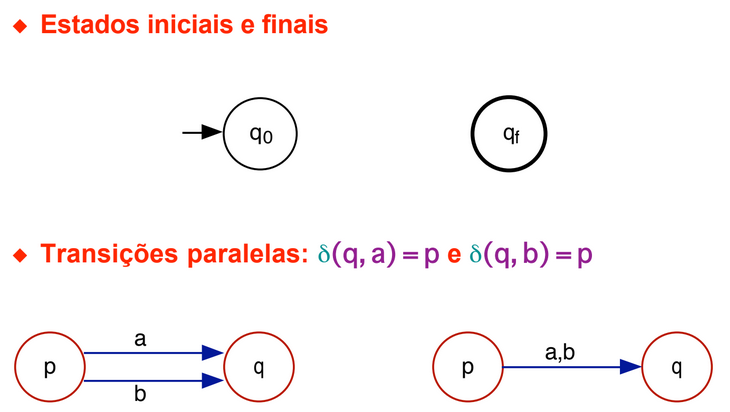
• q0 is a distinct element of Q, the initial state.
• F is a subset of Q, the set of final states.

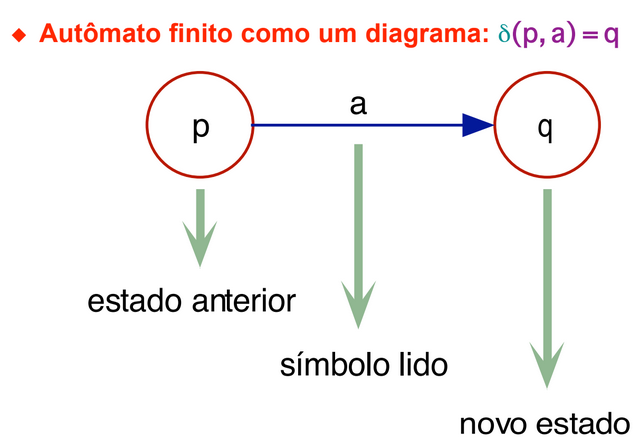
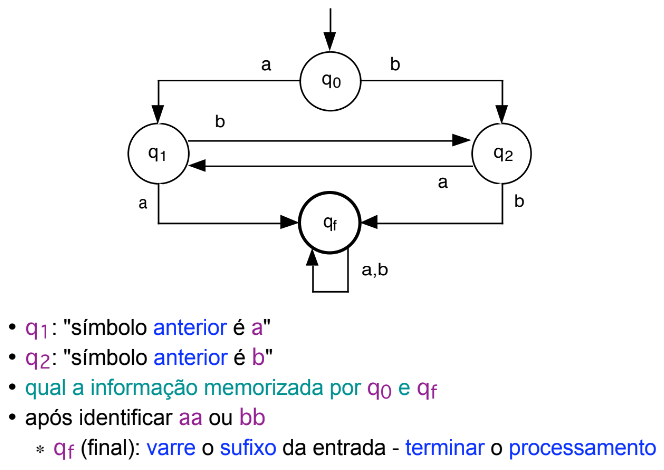
  It is important to note that, in an automaton, if a word does not reach a final state by the end of its processing, it is not part of that grammar. The automaton accepts an input if, after processing the last symbol, it assumes a final state, rejecting it otherwise. Any finite automaton can be viewed as a finite graph (grafo).

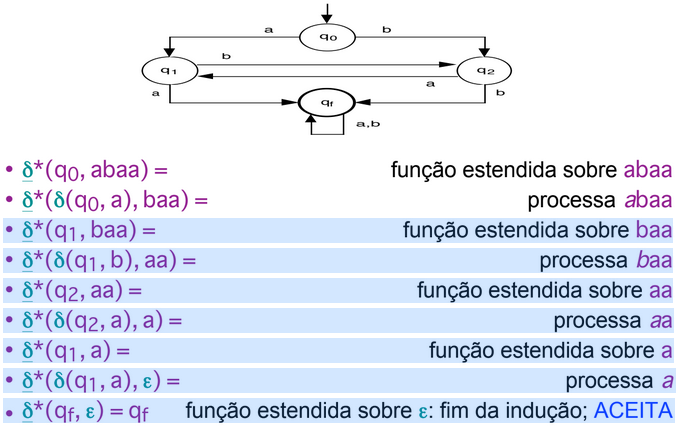
  The sets of accepted and rejected words in an automaton can be represented as:

M = (Σ, Q, δ, q0, F)
• Accepted(M) ∩ Rejected(M) = ∅ (empty set)
• Accepted(M) ∪ Rejected(M) = Σ* (all possible words formed from an alphabet)
• -Accepted(M) = Rejected(M)
• -Rejected(M) = Accepted(M)
Note: if two distinct automatons' Accepted(M) sets are equal, they are Equivalent Finite Automatons.

  If an automaton has no final state, its language will be L = ∅. If an automaton's only state is a final state, then its language will be L = Σ*.

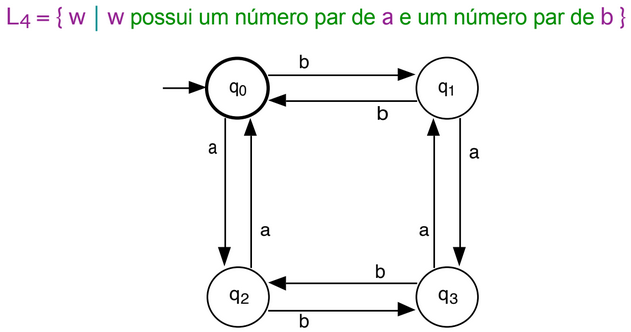
  When it comes to Non-Deterministic Automatons, they may not always be more efficient. They are generally for the study of formal languages, used to determine the capacity to recognize languages and solve problems. Non-determinism in a program is a partial function, such as the transition from one state to a random one when assuming a value. A non-deterministic automaton accepts the entry after processing the last symbol in the tape and there exists at least one final state among the set of alternative states reached. It will reject the entry if all alternative states reached are non-final, or the program is undefined for the argument.

Properties of Regular Languages

Regular Languages (LRs) can be represented by formalisms.

• Low complexity
• Great efficiency
• Easy implementation
• Easy to define non-regular languages
• Limited by its simplicity

Finite automatons belong to the algorithms class. They're more efficient in terms of processing time, and any finite automaton that solves a problem is equally efficient. Redundancy between states may slow it down, but are easily eliminated.

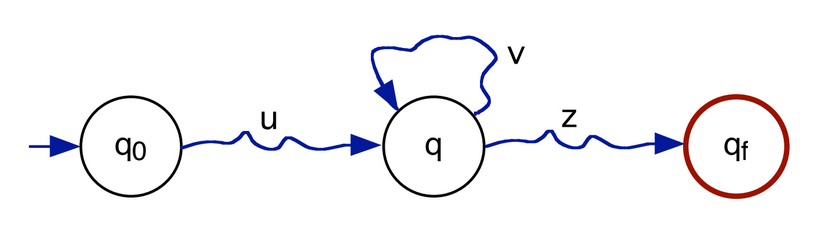
LR "pumping" (bombeamento): if a language is regular, then it's accepted by an AFD of N states. If the automaton recognizes W where len(W) ≥ len(N), assumes any state Q more than once, and there exists a cicle in the function that goes through Q.

W can be divided into three subwords "W = U V Z"

• |U V| ≤ n, |V| ≥ 1
• V is the part of W recognized by the cicle
• The cicle may be executed ("pumped") 0+ times
• For any i ≥ 0, U Vⁱ Z is accepted by the automaton

If the language L is an LR, then there is a constant N such that, for any word W of L where |W| ≥ N, W can be defined as W = U V Z.

• |U V| ≤ N
• |V| ≥ 1

For every i ≥ 0, U Vⁱ Z is a word of L.

An example of "pumping" for LRs:

• N = 4
• W = abbba
• Qr = Qs = ???
• U = ???
• V = ???
• Z = ???

We'll proceed with the example as such:

• Qr = Qs = Q1
• U = a
• V = bb
• Z = ba

You can see that V represents the "repeating" part of the automaton, where a loop is present. If the word W was, for example, "abbbba", then V would be "bbb", as the last "b" is part of the "exit" of the automaton.

Multiple "pumps" may exist at once. A triple pump, for example, may look like:

• { aⁿ b^m a^r | n ≥, m ≥ 0 and r ≥ 0}

To prove a language L is an LR, we may represent it using a regular formalism. Proving otherwise depends on the case, but a useful tool is the use of "pumping".

For example, if you want to prove that L = { W | W contains the same amount of a's and b's} is non-regular: Assume that it IS regular and attempt to prove it through pumping. You'll find that it's impossible, thus it is non-regular. If W = aⁿ bⁿ, where |W| = 2n ≥ n. Therefore, through pumping, W = U V Z:

• |U V| ≤ n
• |V| ≥ 1
• ∀ i ≥ 0, U Vⁱ Z is a word of L

It's an absurd result! Since |U V| ≤ n:

• U V is composed exclusively by symbols "a"
• U V² Z does NOT belong to L (amount of a's is greater than of b's)

Operations can be used over LRs, such as for:

• LR algebra, forming new languages from known ones
• Proving properties
• Constructing algorithms

LR classes are closed for:

• union "⋃"
• concatenation
• complements "∁"
• intersections "⋂"

Unions and concatenation are proven trivially by the definition of a regular expression. Complements are proven by showing that the set of Final States of the complement (Fc) are given by the Total States of the complement (Qc) minus the Final States (F), or Fc = Qc - F, yielding us the non final states of the original Language as final. Upon proving complements, intersections are proven through DeMorgan, where the L1 ⋂ L2 = -(-L1 ⋃ -L2). Since the LR Class is closed for complements and unions, it is also closed for intersections.

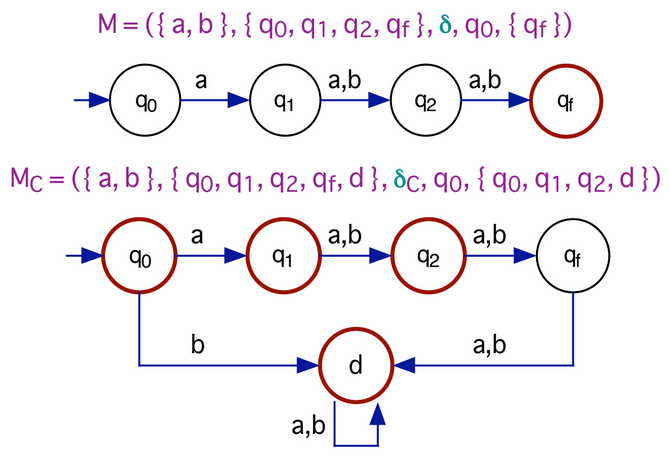
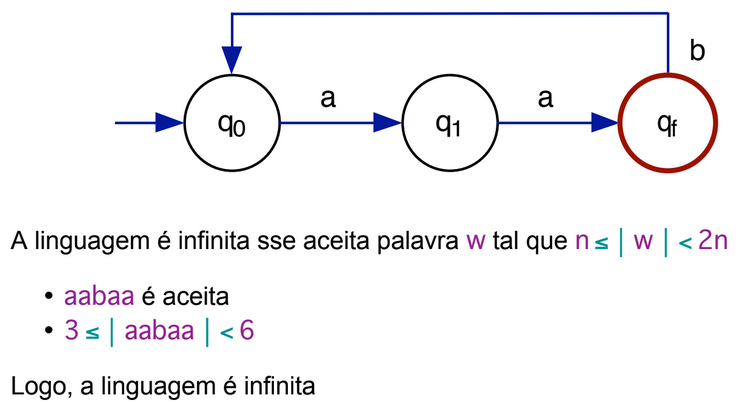
If L is an LR accepted by a finite automaton M = (Σ, Q, δ, q0, F) with n states, then L is:

• EMPTY if, and only if, M does not accept any word W such that |W| < n
• FINITE if, and only if, M does not accept any word W such that n ≤ |W| < 2n
• INFINITE if, and only if, M DOES accept W words where n ≤ |W| < 2n

This is proven by checking if M accepts any word W such that n ≤ |W| < 2n.

• if there exists W ∈ L, it can be defined as W = U V Z
• |U V| ≤ n
• |V| ≥ 1
• ∀ i ≥ 0, U Vⁱ Z is a word of L
Therefore, L is infinite.

If, on the other hand, L is infinite, then there exists W such that |W| ≥ n. It can be proven directly, or through absurdity. The direct proof is simply to show that |W| < 2n. Indirectly would be to use W = U V Z and to try to prove that NO words are shorter than 2n, or |W| < 2n.

Finally, if L is empty, it will process all words of length lower than n. If it rejects all words, the language is empty.

There exists an algorithm to check if two finite automatons are equivalent. They're equivalent if they recognize the same language. The algorithm is described by the following theorem:

Theorem: Equivalence of Regular Languages
If M1 and M2 are AF, then there is an algorithm where ACCEPTED(M1) = ACCEPTED(M2).

Finite Automatons With Outputs

Context Free Languages

Compared to Regular Languages (LRs), Context Free Languages (LLCs) are more ample, their algorithms are simple and have reasonable efficiency. They're mainly applied in artificial languages, like programming ones.

Its uses include:
• Programming Languages
• Syntactic analyzers
• Language translators
• Text processors, in general

Chomsky Hierarchy: The class of LLCs, containing the class of LRs.

LLCs have two approaches:

• Context Free Grammar: Freer than regular grammar, but with production restrictions.
• Stack Automaton: analogous to Finite non-deterministic automatons, has auxiliary memory, supports read and write operations.

The GLCs (Context Free Grammar) make use of derivation trees, with a non-terminal symbol as its root and displaying derivations as branches, while terminal symbols are leaves. Ambiguous grammar can occur, when at least one word has two or more derivation trees to form it.

Creating a Stack Automaton from a GLC: Simple and immediate construction of a recognizer based on the grammar, and its stack structure serves as unique memory, being recognized as a state by Stack Automatons. As a result, states are not necessary to "memorize" past events.

PRODUCING A GLC:
G = (V, T, P, S), where each rule is of form A → α

REMINDER:
• V: finite set of non-terminals
• T: finite set of terminals
• P: union of V and T, finite relation
• S: initial symbol/non-terminal

• A is a variable of V
• α is a word of (V ⋃ T)*

PRODUCING AN LLC:
GENERATE(G) = {w ∈ T* | S → ⁺w}

A "Context Free Language" means that the language is produced through the form A → α.
In a derivation, variable A derives to α without depending

Properties of LLCs

Non-LLC Languages (Linguagens NÃO livres de contexto) are easy to define.

• Duplicate balancing: {ww|w is a word of {a, b}}

Recursive and Context-Sensitive Languages

Class and Language Hierarchies