Linear Systems

  A Linear System of M equations and N variables (m, n >= 1) is a set of equations and variables considered simultaneously. Formatted with rows of equations, we can manipulate it in various ways, such as:

• Adding two lines together to form a third one
• Replacing a variable in one line with its isolated value from another line

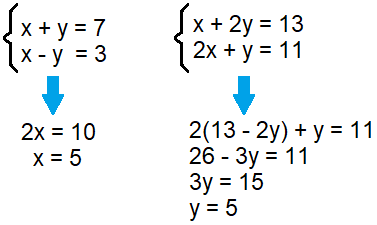
  Besides the interactions between lines, we can also perform three types of operations on the entire equation of each line, in ways that the new systems will have the same solution as the previous one. Those operations are:

• Permutation: switch the lines of the equations



• Multiplication: multiply all coefficients in an equation by a real number



• Summation: Sum one line with the values of another line

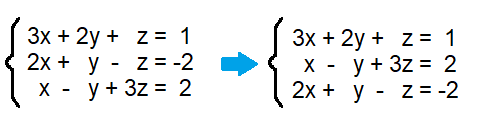
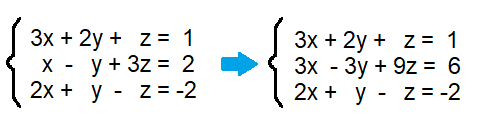
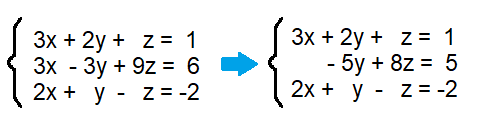
  Through a process called (escalonamento), we can simplify a linear system until it's easier to find the values of the variables. By applying operations to the equations until it has a "staircase"-like shape, we can find each variable at a time for each line in the system. Generally, these systems have either no solution, one solution or infinite solutions.

  An easier way to find the variables in this system is through the Gauss-Jordan method

Matrices

Determinants

  I'm not gonna sugarcoat it, determinants have a lot of lore to them involving permutations of sets of numbers as large as the matrices' dimensions, but we don't care about that. What matters now is calculating them, which is very simple. By "criss cross" multiplying the values, adding the forward crosses and subtracting the backwards ones, we can quickly achieve the determinants of 2nd and 3rd order matrices.

Vector Spaces

  A set V ≠ ∅ is a Vector Space (espaço vetorial) when, and only when:

1 - There is an addition (u, v) -> u + v in V with the following properties:
• u + v < v + u, ∀ u, v ∈ V (commutative / comutativa)
• u + (v + w) = (u + v) + w, ∀ u, v, w &in[ V (associative / associativa)
• There exists a null element for this addition, symbolized generically by 0 (null vector). Therefore, ∃ 0 ∈ V; u + 0 = u, ∀ u ∈ V
• For all elements u ∈ V, its opposite exists, indicated by -u. Therefore, ∀ u ∈ V, ∃ (-u) ∈ V, such that u + (-u) = 0
• For α ∈ ℝ, α * 0 = 0

2 - Multiplication is defined, between ℝ x V in V, as: (α, u) -> α u, where:
• α (β u) = (α β) u
• (α + β) u = α u + β u
• α (u + v) = α u + α v
• 1 u = u
Para quaisquer u, v ∈ V e α, β ∈ ℝ

Examples of vector spaces include:

• ℝ
• ℝ², ℝ³, ..., ℝⁿ
• M_mxn(ℝ)
• P_n(ℝ)
• Let I be an interval of ℝ, indicated by C(I), defined in I and taking real values. Given f, g ∈ C(I) and a ∈ ℝ, f + g and a f are defined as:
  • f + g : I → ℝ and f+g(t) = f(t) + g(t), ∀ t ∈ I
  • a f: I → ℝ e a f(t)

  Vector Subspaces (Subespaços Vetoriais) → Consider V a vector space over ℝ. A vector subspace of V is a subset W ⊂ V such that:

• 0 ∈ W
• ∀ u, v ∈ W, u + v ∈ W
• ∀ α ∈ ℝ, α * u ∈ W

  It can be proven that, if W is a vector subspace of V, then W is a vector space.

  Examples of vector subspaces:
• V and {0}
• P_s(ℝ) is a subspace of P_n(ℝ), 0 ≤ s ≤ n
• A set of simetric matrices is a subspace of M_n(ℝ)

Linear Combination

In ℝ², let u = (1, 2) and v = (2, -1). We have that w = (0, 5) and w = 2 * u + (-1) * v → w = 2u - v. Therefore, we can consider w as a linear combination of u and v.

Generally, given u, v ∈ ℝ², if α₁, α₂ ∈ ℝ such that w = α₁ * u + α₂ * v, then we consider w a linear combination of u and v. Generalizing this idea, we have that:

Let V be a vector space over ℝ. Given the vectors v₁, v₂, ..., v_n, we consider that V is a linear combination of v₁, v₂, ..., v_n if there exists V = α₁ v₁, α₂ v₂, ..., α_n v_n

Let V be a vector subspace over ℝ. We'll consider a set S = {u₁, u₂, ..., u_n} ⊂ V. The set [S] = {α₁ u₁, α₂ u₂, ..., α_n u_n / α₁, α₂, ..., α_n ∈ ℝ}, which is the set of all vectors that can be written as a linear combination of u₁, u₂, ..., u_n is called a subspace generated by S.

Note that [S] = [u₁, u₂, ..., u_n] is a vector subspace of V. We can also say that u₁, u₂, ..., u_n generate S.