Homepage

Calculus

Not much information on calculus will be logged here, only enough to solve methods like Taylor's, whose solving needs N derivatives for the Nth order of the series.

Derivatives

Integrals

Taylor Series

Runge-Kutta Method

We'll take the equation: a₁ f (t + α₁, y + β₁) and expand it to a 2nd order taylor expansion.

a₁ f(t, y) + a₁ α₁ (THINGf/THINGt) + a₁ β₁ (THINGf/THINGy) + a₁ R₁

T⁽²⁾ = f + (h/2) (THINGf/THINGt) + (h/2) (THINGf/THINGy) f, and a₁ = 1; The coefficients' values are α₁ = (h/2) and β₁ = (h/2) f

After equalizing the coefficients, we have that a₁ = 1, therefore:

T⁽²⁾ = f(t + (h/2), y + (h/2) f(t, y)) - R₁

With this, we achieve a much easier to compute equation, with a recursive function as part of it. The error rate of this equation is of the O(h²) order.

The mid-point Runge-Kutta method (método R-K do ponto médio) is, with ω₀ = α (note, this alpha means initial value, so α = y₀ = y(t₀)):

ω_i+1 = ω_i + h f(t_i + (h/2), ω_i + (h/2) f(t_i, ω_i))

T⁽³⁾ ≈ f(t + α₁, y + δ₁ f(t + α₂, y + δ₂ f(y, t)))

For a fourth order Runge-Kutta equation, things get freaky. Here, we implement a more computable process:

ω₀ = α
K₁ = h f(t_i, ω_i)
K₂ = h f(t_i + (h/2), ω_i + (K₁/2))
K₃ = h f(t_i + (h/2), ω_i + (K₂/2))
K₄ = h f(t_i + h, ω_i + K₃)
ω_i+1 = ω_i + (1/6)(K₁ + 2K₂ + 2K₃ + K₄)

This C code solves 4th order Runge-Kutta equation, from t₀ to t₁, needing only that the user changes the function:

#include
#include

double f(double t, double y)
{
return (log(sin(pow(t, y))) + (pow(t, 2) * pow(y, 2))) / sqrt(t);
}

int main()
{
double w, h, t;

printf("\n**********************\n");
printf("\nMETODO DE RUNGE-KUTTA:\n");
printf("\n**********************\n");

printf("Digite o valor inicial do sistema (alfa): ");
scanf("%lf", &w);

printf("Digite o tempo inicial do sistema (t0): ");
scanf("%lf", &t);

printf("Digite o passo do sistema (h): ");
scanf("%lf", &h);

double K1 = h * f(t, w);
printf("\nK1: %lf", K1);

double K2 = h * f(t + (h/2), w + (K1/2));
printf("\nK2: %lf", K2);

double K3 = h * f(t + (h/2), w + (K2/2));
printf("\nK3: %lf", K3);

double K4 = h * f(t + h, w + K3);
printf("\nK4: %lf", K4);

double W1 = ((K1 + (2*K2) + (2*K3) + K4) * (1.0/6.0)) + w;
printf("\nw1: %lf\n\n", W1);

return 0;
}

Consider a method (R-K or Taylor) whose local truncation error (erro de truncamento local), represtented by τ(h), is of the O(hⁿ) order.

ω₀ = α; ω_i+1 = ω_i + h ϕ(t_i, ω_i , h)

Now consier another method with τ'(h) of O(hⁿ⁺¹) order and approximations:

ω'₀ = α; ω'_i+1 = ω'_i + h ϕ'(t_i, ω'_i , h)

Since ω_i = ω'_i = y(t_i), we can restructure the error function:

τ_i+1(h) = { [ y(t_i+1) - y(t_i) ] / h } - ϕ(t_i, ω_i, h)

This equation then becomes: τ_i+1(h) = [ y(t_i+1) - ω_i+1 ] / h, it being analogous to τ'_i+1(h)

After several transformations, we achieve: τ_i+1(h) = τ'_i+1 + (1/h)(ω'_i+1 - ω_i+1), where τ'_i+1 is a very small value. That is because τ_i+1 is of order N (so, for N = 1, an h of 0.1 would still have 0.1 as product), meanwhile τ'_i+1 is of order N+1 (0.1 to the power of 2 would be 0.01, making it 10 times smaller).

At the end, τ_i+1 ≈ (1/h)(ω'_i+1 - ω_i+1)

In practice, to limit τ_i+1 by ε (a given tolerance), we calculate a value q:

q = [ (ε h) / ( |ω'_i+1 - ω_i+1| ) ]^(1/n);

Note that, here, N = order (So Euler's method would have N = 1, an R-K of order 2 would have N = 2, etc. Euler, R-K and Taylor may be used here).

If q is smaller than 1, then a bad value for h was chosen, likely very big. If q is greater than 1, the entry may be accepted, but the next step should be (q * h). Ideally, q = 1, in which case the best amount of steps (h) was chosen.

Now, obersving the Runge-Kutta-Fehlberg method, it is used with the 4th or 5th order of Runge-Kutta, where each of the Ks is multiplied by specific coefficients. There'd normally be 9 Ks to calculate, but these changes permit only needing to calculate up to K6, with no K2 (although it's still needed to find K3):

ω'_i+1 = ω_i + (16/135)K1 + (6656/12825)K3 + (28561/56430)K4 - (9/50)K5 + (2/55)K6

ω_i+1 = ω_i + (25/16)K1 + (1408/2565)K3 + (2197/4104)K4 - (1/5)K5

The equations for each K are:

holy fuck

Multistep methods

y' = f(t, y(t)); a ≤ t ≤ b; y(a) = α

ω_i+1 = a_m-1 ω_i + a_m-2 ω_i-1 + a_m-3 ω_i-2 + ... + a₀ ω_i+1-m + h[b_m f(t_i+1, ω_i+1) + b_m-1 f(t_i, ω_i) + b_m-2 f(t_i-1, ω_i-1) + ... + b₀ f(t_i+1-m, ω_i+1-m)]

m is the number of steps and is an integer greater than 1. (An m = 1 would be a one-step method)

∫(from t_i to t_i+1) y' dt = ∫(from t_i to t_i+1) [f(t, y(t)) dt]

y(t_i+1) - y(t_i) = ∫(from t_i to t_i+1) [f(t, y(t)) dt]

y(t_i+1) = ∫(from t_i to t_i+1) [f(t, y(t)) dt] + y(t_i)

Adams-Bashforth Two Step Explicit Method (Método Explícito de Adams-Bashforth de dois passos):

ω₀ = α₀; ω₁ = α₁

ω_i+1 = ω_i (h/2) [3 f(t_i, ω_i) - f(t_i-1, ω_i-1)] → τ(h) = O(h²)

Predictor-Corrector Scheme (Esquema Preditor-Corretor)

Uses the M Step Explicit Method to find the prediction and uses the M-1 Step Implicit methor to correct the prediction. Note that both methods are of τ(h) = O(h^m) order.

In this Predictor-Corrector Scheme, ω⁽⁰⁾_i+1 and ω⁽¹⁾_i+1, where (0) indicates predictor, and (1) indicates corrector

Example: 4 Step Explicit and 3 Step Implicit on the Predictor-Corrector Scheme y' = t e^3t + 2 y

Finite Linear Differences

y''(x_i) ≈ (1/h²)[y(x_i+1) - 2y(x_i) + y(x_i-1)] -> Finite CENTERED Differences (Diferenças finitas centradas) of 2° order.

y'(x_i) ≈ (1/2h)[y(x_i+1) - y(x_i-1)] -> Finite Centered Differences

y'' = -(y')² - y + ln(x); 1 ≤ x ≤ 2; y(1) = 0; y(2) = ln(2); h = 0.25;

y''i ≈ (1/h²)(ωi+1 - 2ωi + ωi-1)
y'i ≈ (1/2h)(ωi+1 - ωi-1)

P/x1 : (1/h²)(ω2 - 2ω1 + 0) + (1/4h²)(ω2² - 2ω2 * 0 + 0) + ω1 - ln(1.25) = 0

P/x2 : (1/h²)(ω3 - 2ω2 + ω1) + (1/4h²)(ω3² - 2ω3 * ω1 + ω1²) + ω2 - ln(1.5) = 0

P/x3 : (1/h²)(ln(2) - 2ω3 + ω2) + (1/4h²)(ln(2)² - 2ln(2) * ω2² + ω2²) + ω3 - ln(1.75) = 0

Matriz Jacobiana (J):

(-2/h²) + 1 | (1/h²) + (ω2/2h²) | 0

(1/h²) + [(-ω3 + ω1)/2h²] | (-2/h²) + 1 | (1/h²) + [(ω3 - ω1)/2h²]

0 | (1/h²) + [(-ln(2) + ω2)/2h²] | (-2/h²) + 1

Para montar a equação de formato x^(k+1) = x^(k) - J(x^(k)) F(x^(k)), precisamos agora do vetor F(x^(k))

ω⁽⁰⁾ = [ω1⁽⁰⁾ , ω2⁽⁰⁾ , ω3⁽⁰⁾] -> [0 , 1 , -1]

J(ω⁽⁰⁾), com o chute inicial (valores de ω):

-31 | 24 | 0

24 | -31 | 8

0 | 18.4548 | -31

F(ω⁽⁰⁾), usando os valores de ω nas funções dadas (P/x):

Eq. geral: 16(ωi+1 - 2ωi + ωi-1) + 4(ωi+1² - 2ωi+1 * ωi-1 + ωi-1²) + ωi - ln(x) = 0

16(1 - 0 + 0) + 4(1 - 2 * 0 + 0) + 0 - 0.2231 = 19.7769

16(-1 -2 + 0) + 4(1 + 2 * 0 + 0) + 1 - 0.4054 = -43.4054

16(0.6931 + 2 + 1) + 4(0.4803 - 1.3862 * 1 + 1) + -1 - 0.5596 = 57.9074

Agora, suponha que J z = F. Com J sendo nossa Jacobiana e F sendo o vetor que acabamos de calcular:

[ -31 | 24 | 0 ] [z1] = [ 19.7769]

[ 24 | -31 | 8 ] [z2] = [-43.4055]

[ 0 | 18.4548 | -31 ] [z3] = [ 57.9074]

[ -31 | 24 | 0 ] [z1] = [ 19.7769]

[ 24 | -31 | 8 ] [z2] = [-43.4055]

[ 0 | 18.4548 | -31 ] [z3] = [ 57.9074]

Com isso, temos que [z1 , z2 , z3] = [ 0.6917 , 1.7175 , -0.8455]

Finalmente, teremos que ω⁽¹⁾ = ω⁽⁰⁾ - z

ω⁽¹⁾ = [ 0 , 1 , -1] - [ 0.6917 , 1.7175 , -0.8455]

ω⁽¹⁾ = [ -0.6917 , -0.7175 , -0.1545]

Class Notes

These are simply the transcripts (in portuguese) of the class notes my professor has taken, for us to revise as needed.

1. Problema de valor inicial para Equações Diferenciais Ordinárias. A quase totalidade dos fenômenos físicos que observamos ao nosso redor são descritos matematicamente através de Equações Diferenciais. A este procedimento dá-se o nome de modelagem matemática, ou simplesmente modelagem. As Equações Diferenciais resultantes podem ser ordinárias ou parciais, lineares ou não lineares e de ordens diferentes. A grande maioria destas equações não possuem solução analítica e só podem ser resolvidas aproximadamente, utilizando-se métodos numéricos e suas implementações computacionais correspondentes, apropriadas para este fim. No que se segue, iremos estudar métodos de soluções computacionais para EDOs (no tempo), lineares ou não lineares, de primeira ordem. A generalização para sistemas de equações de 1° ordem e para equações de ordem superior será abordada posteriormente.

1.1 - Método de Euler

Apesar do método de Euler ser raramente utilizado na prática, a simplicidade de uma dedução pode ser usada para ilustrar a lógica por trás da dedução das técnicas mais sofisticadas. O objetivo do método é obter uma aproximação para a solução do problema de valor inicial:

^dy⁄_dt = f(y, t), a ≤ t ≤ b e y(a) = α

Primeiro, vamos investigar graficamente o problema:

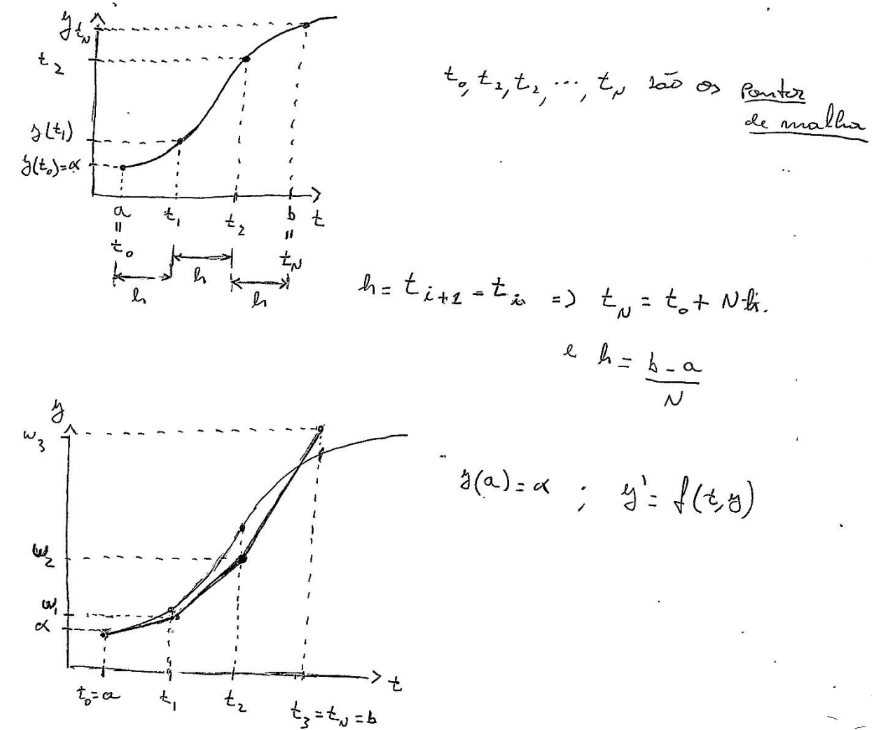
Vamos deduzir o método utilizando o teorema de taylor:

y(t_i+1) = y(t_i) + (t_i+1 - t_i) y'(t_i) + [(t_i+1 - t_i)² / 2] y'' (ξ_i)

Para algum ξ_i em [t_i, t_i+1] como h = t_i+1 - t_i

=> y(t_i+1) = y(t_i) + h y'(t_i) + (h/2)² y'' (ξ_i), onde y'(t_i) = f(y, t)

=> y(t_i+1) = y(t_i) + h f(y(t_i), t_i) + (h/2)² y'' (ξ_i), onde y'(t_i) = f(y, t)

Então o método de Euler aproxima y(t_i+1) por excluir termos de ordem superior.

ω₀ = α ; ω_i+1 = ω_i + h f(t_i, ω_i) para cada i = 0, 1, 2, ..., N-1

A equação acima é chamada equação de diferença associada ao método de Euler. Exemplo: y' = y - t² + 1 ; aproxime y para 0 ≤ t ≤ 2 ; y(0) = 0.5. Vamos fazer N = 10, ou seja, h = 0.2, t_i = 0.2 i ; t_N = 2.0 e t₀ = 0.0. Começamos o nosso procedimento computacional fazendo ω₀ = y(t₀) = 0.5. Agora, conforme indicado na equação de diferença associada ao método de Euler: